| |
 |
|
|
Was ist der Goldene Schnitt?
|
Ein für alle klaren und wissbegierigen
Geister nothwendiges Werk; wo jeder Studierende
der Philosophie, Perspective, Malerei, Sculptur,
Architektur, Musik und anderer mathematischer
Fächer eine angenehme subtile und bewundernswerthe
Gelehrsamkeit antreffen und sich mit verschiedenen
Fragen der heiligsten Wissenschaft erfreuen wird.
Luca Pacioli (De Divina Proportione,
1509)
|
Der Goldene Schnitt (lat. sectio aurea) ist ein
bestimmtes Verhältnis zweier Zahlen (meist
Längen von Strecken), das in der Kunst und
Architektur oft als ideale Proportion und als
Inbegriff von Ästhetik und Harmonie angesehen
wird. Darüber hinaus tritt es auch in der
Natur in Erscheinung und zeichnet sich durch eine
Reihe interessanter mathematischer Eigenschaften
aus. Schon lange bevor man ihn Goldenen Schnitt
nannte, wurde er auch stetige Teilung oder göttliche
Teilung (lat. proportio divina) genannt.
Wie konstruiert man nun den Goldenen Schnitt?
Ein Punkt T teilt eine Strecke AB dann im Goldenen
Schnitt, wenn sich die größere Teilstrecke
zur kleineren verhält wie die Gesamtstrecke
zum größeren Teil. Also AT : TB = TB
: AB. Der größere Teil der Strecke
wird meist mit Major, der kleinere mit Minor bezeichnet.
Wenn wir Major durch Minor teilen ergibt das einen
Wert, den wir Phi nennen?
Auf Phi kommt man auch durch die Gleichung:
½•(1+sqrt(5)) =
1,61803398874989484820458683436563811772030917980576286...
Doch genug der Theorie, jetzt wird gezeichnet!
|
|
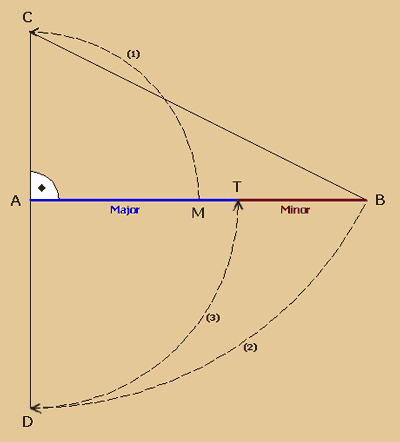
Eine Konstruktion
der inneren Teilung bedeutet, dass eine bestehende
Strecke durch einen zu konstruierenden Punkt im
Goldenen Schnitt geteilt wird. Wieder einmal war
es Euklid, von dem diese bekannte Teilungsart
überliefert ist. |
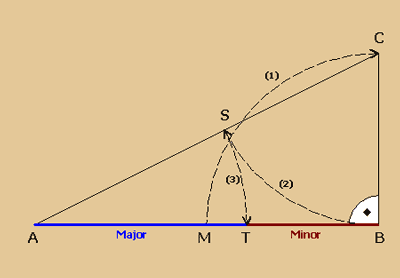
Eine andere Teilungsart stammt von Heron von Alexandria:
|
|
|
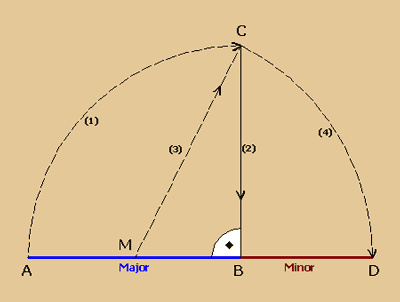
Eine äußere Teilung
liegt vor, wenn die bestehende Teilstrecke selbst
Major oder Minor einer durch einen zu konstruierenden
Punkt entstehenden Gesamtstrecke ist, wie hier
zu sehen.
|
|
|
|
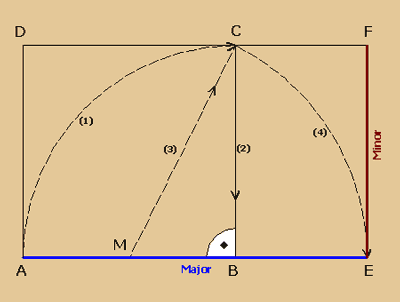
In der Abbildung hier sehen
wir die Konstruktion eines Rechteckes mit den
Maßen des Goldenen Schnittes.
|
|
|
|
|
|
 |
| |
 |
Was ist der Goldene Schnitt? |
|
|
|
|
|
|
|
| |
| |
|