Die Geometrie ist vor der Erschaffung der Dinge, gleich ewig wie der Geist Gottes selbst und hat in ihm die Urbilder für die Erschaffung der Welt geliefert.
Johannes Kepler (Harmonices Mundi, 1619)

Die Geschichte des Goldenen Schnittes ist schon sehr alt. So alt, dass es nicht mal eine einstimmige Meinung darüber gibt, auf wen er denn nun eigentlich zurückzuführen ist. Ich denke, auch wenn Euklid der erste war, der seine Studien um den Goldenen Schnitt ausführlich niederschrieb und erläuterte, gebührt der Ruhm des Entdeckers aber doch dem ca. 100 Jahre vor ihm gelebten Hippasos von Metapont. Dieser Mathematiker gab für den Goldenen Schnitt nicht nur seine eigene Weltanschauung auf, der Legende nach wurde er dafür sogar von seinen Kollegen aus dem Pythagoräischen Bund öffentlich ermordet.
Aber neben Hipassos haben sich noch viele andere mehr oder weniger berühmte Leute mit dem Goldenen Schnitt beschäftigt. Die folgende Aufzählung hat mit Sicherheit keinen Anspruch auf Vollständigkeit. Dennoch habe ich versucht mal die wichtigsten Personen um den Goldenen Schnitt chronologisch aufzulisten. Here they are!

Hippasos von Metapont

Hippasos von Metapont lebte um 450 v.Chr. Er war ein Mitglied der "Pythagoräer", eines Wissensbundes, der der absoluten Überzeugung war, dass die Welt sich vollständig durch ganze Zahlen beschreiben lassen müsse. Ihr Begründer war, wie man sich denken kann, Pythagoras, der bereits 120 Jahre zuvor Gesetze in der Geometrie ausgemacht hatte, die bis heute unser mathematisches Leben bestimmen, wie z.B die Längenverhältnisse in rechtwinkligen Dreiecken. Aber zurück zu Hipassos. Wie Pythagoras glaubte auch er, dass die Struktur der Welt sich auf rationale Zahlen und deren Verhältnisse gründen müsse. Schon Pythagoras entdeckte, dass sich genau der gleiche Ton eine Oktave höher ergibt, wenn eine Saite im Verhältnis 1:1 geteilt wird. Durch andere ganzzahlige Teilverhältnisse lassen sich beliebige Tonintervalle erzeugen, wie sie noch heute in den Dur- und Moll-Tonleitern üblich sind.
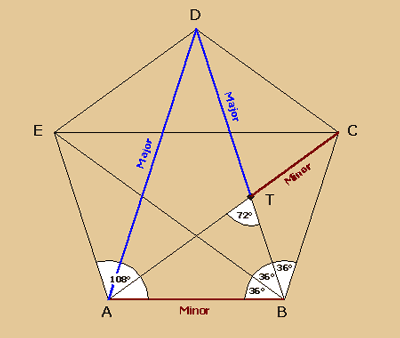
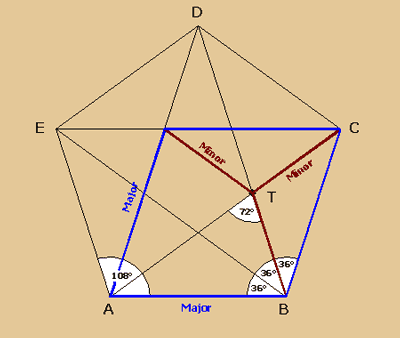
Das Pentagramm, ein fünfzackiger Stern, der in einem gleichseitigen Fünfeck eingeschlossen ist, war seit jeher das Erkennungszeichen des pythagoräischen Bundes und stand ursprünglich für die Suche nach der universalen Wahrheit. Es entbehrt nicht einer gewissen Ironie, dass Hipassos ausgerechnet in diesem Pentagramm die Widerlegung der Ansicht der Pythagoräer fand. Er entdeckte, dass sich die Diagonalen in einer ganz besonderen Art und Weise schneiden. Der Teilpunkt liegt so, dass sich die größere Teilstrecke zur kleineren so verhält wie die Gesamtstrecke zum größeren Teil.

Euklid (325-270 v.Chr.)

Auf seiner Suche nach einfachen Möglichkeiten, um Netze Platonischer Körper zu konstruieren, fand Euklid in älteren Schriften, Hipassos’ Wissen wieder, dass im regulären Fünfeck ein erstaunliches Streckenverhältnis vorliegt. Euklid war der erste, der es nach ausgiebiger analytischer Auseinandersetzung in seinem II. Buch der "Elemente" in Satz 11, mit "proportio habens medium et duo extrema", heute übersetzt als "Teilung im inneren und äußeren Verhältnis" erklärte und zusammen fasste.

Leonardo Fibonacci war der Sohn eines Kaufmanns aus Pisa, der mit arabischen Ländern in Nordafrika Handel trieb. Sein Vater war der Leiter der pisanischen Handelskolonie in Bugia im heutigen Algerien. Dadurch hatte Fibonacci muslimische Lehrer und reiste u. a. nach Ägypten, Syrien und Griechenland. Ca. 200 Jahre bevor sich das Dezimalsystem in Europa durchgesetzt hatte, studierte er die hindu-arabischen Ziffern, unsere heutigen “arabischen Zahlen“ und die von arabischen Mathematikern entwickelten Rechenmethoden. 1202 entstand sein wichtigstes Werk, der “Liber abaci“, ein enzyklopädisches Rechenbuch, das der westlichen Welt die arithmetischen Rechenmethoden auf der Basis des indisch-arabischen Stellenwertsystems vermittelte. Mit diesem Werk führte Fibonacci die Zahl 0 im Abendland ein. Fibonacci war Mathematiker am Hof Kaisers Friedrich II und verfasste zahlreiche geometrische und zahlentheoretische Schriften, die seiner Zeit oft weit voraus waren. Seine wohl folgenreichste Leistung war die umfassende Darstellung und Erläuterung des Rechnens mit den damals noch nicht gebräuchlichen indisch-arabischen Ziffern. Für viele gilt Leonardo Pisano als der bedeutendste Mathematiker des Mittelalters.
Er entdeckte den gesetzmäßigen Ablauf des Wuchsverhaltens von Pflanzen und dass dieses Zahlenkonzept auch in allen anderen biologischen Bereichen wieder zu finden ist. Dieses Konzept ist heute in der ganzen Welt als Fibonacci-Reihe bekannt. Beginnend bei 0, wird sie errechnet, indem man immer die letzten zwei Zahlen addiert, um die nächste Zahl der Reihe zu erhalten:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...
(1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13...)
Wenn man innerhalb der Fibonacci-Reihe eine Zahl durch die vorhergehende Zahl dividiert, erhält man einen Wert, der der transzendenten Zahl Phi (0,6180339...) umso näher kommt, je höher die Zahlenwerte aus der Fibonacci-Reihe sind:
1 geteilt durch 1 = 1
2 geteilt durch 1 = 2
3 geteilt durch 2 = 1,5
5 geteilt durch 3 = 1,66
8 geteilt durch 5 = 1,60
13 geteilt durch 8 = 1,625
21 geteilt durch 13 = 1,615
34 geteilt durch 21 = 1,619
55 geteilt durch 34 = 1,617
89 geteilt durch 55 = 1,6181
Die Ergebnisse nähern sich Phi immer weiter an, bis ein Unterschied fast nicht mehr nachvollziehbar ist.

Luca Pacioli di Borgo San Sepolcro war Mönch. Er entdeckte die Werke von Euklid wieder und lehrte sie. Er erkannte, dass die Streckenteilung der gleichen inneren und äußeren Teilung elementar für die Konstruktion der Netze Platonischer Körper war. Er nannte sie die “Divina Proportione“ - Göttliche Teilung. Göttlich, so sagte er, weil sie einzigartig sei und ihr Wesen mit nichts anderem verglichen werden könne - darin sei sie wie Gott. Auch sein großes Werk, in dem er sich mit Euklid und seinen Lehren auseinander setzte, trägt diesen Namen. Für dieses Buch schuf Leonardo da Vinci (1471-1528) 60 Illustrationen. Auch die berühmte Zeichnung über die Quadratur des Kreises wird auf die Arbeit an der “Divina Proportione“ zurückgeführt. Die Idee zu dieser Skizze stammt allerdings weder von Leonardo, noch von Pacioli, sondern von dem römischen Architekten Marcus Vitruvius Pollio, der bereits 84 v.Chr. geboren wurde.
Nebenbei: Pacioli hat sich die Doppelte Buchführung ausgedacht und ist somit der Erfinder des modernen Rechnungswesens in Unternehmen.

Johannes Kepler war der erste Autor, der nicht nur die mathematische Beziehung zwischen dem Goldenen Schnitt und der Fibonacci-Folge erkannte, sondern beide auch mit Elementen der belebten Natur verband.
In der theoretischen Himmelsmechanik spielt der Goldene Schnitt und damit die Zahl Phi=1,61803399... eine gewisse Rolle. Sie ist die am schlechtesten durch einen Bruch anzunähernde irrationale Zahl und weit widerspenstiger als PI=3,14159...
Wie schon Luca Pacioli und sein Mitstreiter Leonardo da Vinci zeigten, stößt man überall bei der Morphologie der Lebewesen, ihrem Wachstum, ihren Bewegungen und ihrer inneren Struktur auf die geometrischen Beziehungen des Goldenen Schnitts. Dagegen kommt der Goldene Schnitt in unbelebten Prozessen gewöhnlich nicht vor, zumindest nicht auf der Ebene der sichtbaren Körper auf der Erde.
In diesem Rahmen gelang es Johannes Kepler, die Anomalien der Planetenbewegungen aufzuklären. Damit setzte er eine Revolution in Physik und Mathematik in Gang. Indem er zeigte, dass der Mars keine kreisförmige, sondern eine nahezu elliptische Bahn verfolgt, schuf Kepler ein Paradox. Wenn die Bahn eines Planeten nicht kreisförmig ist und damit keine einfache mathematische Funktion hat, sondern sich in jedem beliebig kleinen Intervall auf nichtlineare Weise ändert, woher weiß dann der Planet, wie er sich bewegen soll? Die Umlaufbahn und die Umlaufgeschwindigkeit müssen die Wirkung eines Prinzips ausdrücken, das nicht einer genauen mathematischen Zahl oder Funktion entspricht, aber dennoch eine eindeutige Existenz aufweist. Das nannte Kepler den "Geist des Planeten“.
Nur nebenbei bemerkt begründete Kepler in seinem Aufsatz über die "Schneeflocke" die Methode der Kristallographie, die der experimentellen Wissenschaft erstmals die Möglichkeit eröffnete, vom makroskopischen in den mikroskopischen Bereich als Grundlage für morphologische Unterscheidungen lebender und nicht lebender Prozesse auf makroskopischer Ebene einzudringen. Diese Methode benutzte Mendelejew später zur Ableitung des Periodensystems der chemischen Elemente.

Um das berühmte Verhältnis des Goldenen Schnitts 1:1,618… auszudrücken benutzen wir die Bezeichnung Phi. Man nimmt an, dass dies von der Verherrlichung der Griechischen Leistungen im Allgemeinen her rührt. Phi kommt hierbei von Phidias, dem griechischen Bildhauer und Architekten, unter dessen Leitung der Parthenon-Tempel in Athen gebaut wurde. In seiner Ruine finden sich vielfache Hinweise und Abmessungen des Goldenen Schnittes.

Der Begriff "Goldener Schnitt" als solcher taucht zum ersten Mal 1835 in Martin Ohm’s zweiter Auflage seines mehrbändigen Werks "Die reine Elementar-Mathematik, weniger abstrakt, sondern mehr anschaulich" auf. Ab jetzt hat die über so viele Jahrhunderte von so vielen klugen Denkern verehrte und von Pacioli göttlich genannte Streckenteilung endlich einen Namen.