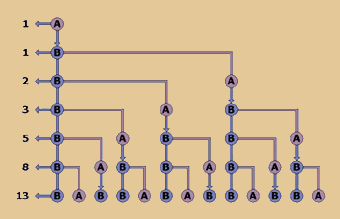
Man stelle sich vor, ein Lebewesen (A) z.B. benötigt einen Tag, um geschlechtsreif (B) zu werden. Und nach einem weiteren Tag setzt dieses Lebewesen ein weiteres in die Welt. Dieses wird wiederum nach einem Tag erwachsen, setzt dann wieder ein Lebewesen in die Welt usw.

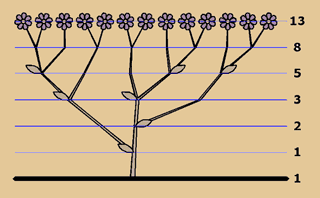
Wenn wir eine solche Population in Zahlen ausdrücken wollen, erhalten wir eine Zahlenreihe, die von Leonardo Fibonacci di Pisa entdeckt wurde, als er gerade das Wuchsverhalten von Pflanzen untersuchte und deshalb nach ihm benannt wurde. Auch hier können wir das Verhalten der Natur beobachten, die neue Triebe oder Samen nach der Fibonacci-Zahlenreihe bildet.

Benutzen wir die Zahlen und wenden sie in Längen- und Breitenverhältnissen von Dreiecken an, können wir daraus eine Spirale zusammensetzen.

Diese Spiralen finden wir in der Natur sehr häufig an. Bei der Nautilusschnecke kann man sie wohl am deutlichsten erkennen.

Viele Pflanzen ordnen ihre Samen so an, dass man von einem Zentrum ausgehend rechtsdrehende und linksdrehende Spiralen abzählen kann. Erstaunt stellt man fest, dass die Anzahlen der rechts- und der linksdrehenden Spiralen stets zwei aufeinander folgende Fibonacci-Zahlen sind. Dies hängt damit zusammen, dass das Keimzentrum den jeweils nächsten Samen, oder an einem Stängel das jeweils nächste Blatt bzw. den jeweils nächsten Seitentrieb, immer um den Goldenen Winkel versetzt entstehen lässt.
Die Winkel zwischen zwei nacheinander entstandenen Samen betragen nämlich etwa 137.50 und 222.50. Diese Winkel teilen den vollen Kreis im Verhältnis des Goldenen Schnitts:

Dieses Verhältnis wiederum kann am Besten durch zwei aufeinander folgende Fibonacci-Zahlen angenähert werden. Die Pflanzen wählen den Goldenen Winkel vermutlich, weil mit ihm auf kleiner Fläche viele Samen untergebracht werden können. Aber eigentlich weiß man das überhaupt nicht.
Sieht man sich den Fruchtstand einer Sonnenblume genauer an, erkennt man, dass die Kerne in spiralförmigen Linien angeordnet sind. Es gibt links- und rechtsdrehende Spiralen. Zählt man die linksdrehenden, so stößt man auf die nach Fibonacci benannten Zahlen, also 21, 34, 55, 89, 144, 233 ... . Erstaunlicherweise ergibt die Anzahl der rechtsdrehenden Spiralen nicht die gleiche, sondern eine benachbarte Fibonacci-Zahl. Das Verhältnis der beiden Summen entspricht einer Annäherung an den goldenen Schnitt.

Dieses Phänomen können wir auch bei unzähligen anderen Erscheinungsformen in der Natur beobachten. Als Beispiele seien hier Pinienzapfen, Kakteen, Brokkoli und Gänseblümchen genannt.
Anhand dieses strikten mathematischen Aufbaus unserer gesamten Natur drängt sich mir ein Gedanke auf. Da hat doch jemand unsere Entwicklung gemäß der Fibonacci-Reihe ausgezählt, oder was?!
In dieser konsequent überlebensstrategischen Selektion zeigt sich die Weisheit der Natur, ohne uns zu enthüllen, wieso sie sich so verhält. Uns ist nur bekannt, dass es sich weder um einen Zufall noch um einen Wettbewerbsvorteil handelt gegenüber Organismen, die solch eine Anordnung ihrer Spiralen nicht haben. Aber warum die Spiralenzahl nicht gelegentlich 87 statt 89 oder 12 statt 13 ist, dieses Geheimnis konnten wir der Natur bisher noch nicht entlocken. Was uns bleibt ist weiterhin ihre ästhetische Weisheit zu bewundern und staunend Kenntnis zu nehmen von der zauberhaften Selbstorganisation des Lebendigen.