Ein Hypercube, oder auch Hyperwürfel ist ein regulärer mehr-, mindestens aber vierdimensionaler Würfel. Damit ist schnell gesagt, was ein Hypercube ist. Aber wie er aussieht, dazu bedarf es ein klein wenig mehr Mühe, die zu machen, ich mich nicht gescheut habe:
Beim näheren Beschäftigen mit unserem neuen vierdimensionalen Freund, fiel mir eines ganz schnell auf. Alle Versuche, den Hypercube darzustellen, sind im Grunde von vorn herein unzureichend. Durch meine Arbeit als Bauzeichnerin bin ich sehr vertraut mit der zweidimensionalen Darstellung von Körpern. Als ich aber nun damit begann, mir einen vierdimensionalen Körper vorzustellen und vor allem ihn abzubilden, wurde mir schnell klar, dass dies ungleich schwieriger war. Wir schummeln ja schon, wenn wir nur dreidimensionale Körper darstellen wollen… Ich glaube, am besten ist, wir tasten uns einfach langsam ran und beginnen dabei mal ganz von vorn. Am Anfang war das Nichts…

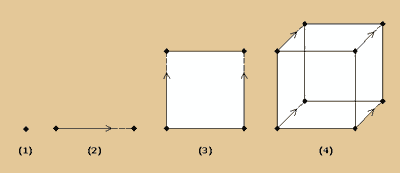Ein Punkt hat keine Dimension (1). Dehnen wir den Punkt in eine Richtung aus, erhalten wir eine Linie (2) und die hat jetzt eine Dimension. Nun verschieben wir unsere Linie auf dem Papier nach oben und schon haben wir ein Quadrat mit zwei Dimensionen (3). So, und jetzt geht die Schummelei schon los... Um die dritte Dimension auf einem Blatt Papier überhaupt darstellen zu können, müssen wir uns mit einem Trick behelfen. Wir verschieben unser Quadrat in einem Winkel von 45° nach hinten (4). Die Strecke, die später die Eckpunkte verbindet, darf dabei nur halb so lang sein, wie die Kantenlängen des Quadrats, da sonst nicht der optische Eindruck eines Würfels entstehen würde. Kritiker der Parallelprojektion maulen daran zwar herum, aber ich finde sie für unsere Zwecke allemal anschaulicher als z.B. die Isometrie. 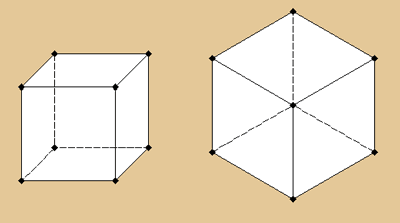Bei dieser werden die nach hinten verschobenen Seitenflächen des Würfels zwar in Originallänge abgebildet, dafür beträgt der Winkel der Grundkante und der Verbindungslinien unseres Quadrates jeweils 30°. Hier sehen wir eine Parallelverschiebung und eine Isometriesche Darstellung eines Würfels.

Durch den 30° Winkel sieht unser Würfel in der Isometrie aus wie ein regelmäßiges Sechseck, dass in drei gleich große Parallelogramme oder - wenn man die unsichtbaren (gestrichelten) Kanten mitzählt - in sechs gleiche Dreiecke aufgeteilt ist. 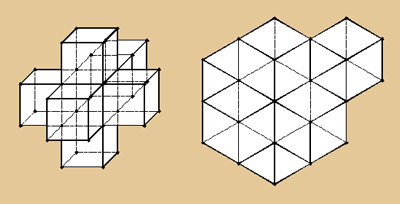Bei einem einfachen Würfel mag das noch ganz übersichtlich sein, aber wenn wir uns ein etwas komplexeres Gebilde wie den Tesseract ansehen, dann sieht die Isometrie nicht mehr ganz so durchschaubar aus. Links die Parallelprojektion, rechts die Isometrie

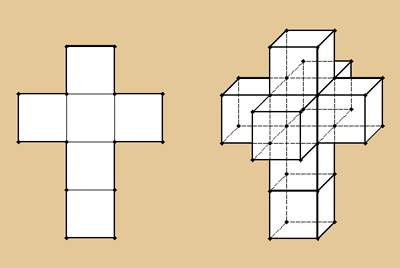
Der Tesseract ist nicht zufällig als Beispiel gewählt. Er spielt im Zusammenhang mit dem Hypercube eine wichtige Rolle. Er ist sein Netz. Zum besseren Verständnis: Wenn wir einen Würfel auseinander falten, erhalten wir ein zweidimensionales Netz des Körpers. Insgesamt gibt es von einem Würfel elf verschiedene Netze. Das bekannteste davon ist das Kreuz. Der Tesseract ist das Netz des Hypercubes. Er ist seine Auffaltung in die dritte Dimension. In seinem Fall gibt es allerdings insgesamt 261 verschiedene Netze. Hier sehen wir links ein Netz des Würfels und rechts ein Netz des Hypercubes.