Ich könnte jetzt ganz schlaumeierisch daher kommen und sagen: Die Hamming-Distanz ist die kleinste auftretende Distanz zwischen zwei Codeworten innerhalb eines definierten Codes. Sie gibt an, wie viele Bits sich ändern müssen, damit ein neues, gültiges Codewort entsteht. Aber ich glaube, damit ist demjenigen, der mit Hamming bisher wirklich auf Distanz war, in der Tat nicht geholfen.
Im Hinblick, dass seine Methode heute in nahezu jedem Rechner, CD-Spieler oder Handy angewendet wird, um Übertragungsfehler zu erkennen und sogar zu beheben, hat Richard Wesley Hamming, als er die gleichnamige Distanz Anfang der 50er Jahre einführte, der Entwicklung der Technik einen wahren Dienst erwiesen. Alles hatte in der Nachrichtenübertragung seinen Anfang. Schickt man eine Nachricht bestehend aus vielen kleinen Informationsbits auf die Reise, kann eine Menge passieren. Da ein binärer Code ja nur aus Nullen und Einsen besteht, kann man sich gut vorstellen, was passiert, wenn diese sich auf ihrer Reise mal vertauschen: Die Nachricht ist nicht mehr lesbar. Um dieser misslichen Lage zu entkommen, hat sich Mr. Hamming folgendes ausgedacht. Er baute in den Code so genannte Prüfbits ein. Also statt einer Null schickt man drei Nullen auf die Reise und statt einer eins auch drei Einsen. Was davon jetzt beim Empfänger ankommt, wird nach dem Mehrheitsprinzip ausgewertet. Bedeutet, wenn zwei von drei Zahlen Null sind, wir die ganze Gruppe als Null interpretiert. Dabei gilt natürlich, je mehr Prüfbits in einem Code vorhanden sind, umso mehr Fehler können erkannt und sogar korrigiert werden. Die Hamming-Distanz ist also quasi der Abstand zwischen einer gesendeten und einer fehlerhaft empfangenen Bitfolge. Die Hamming-Distanz wird umso größer, je größer die Anzahl der Übertragungsfehler ist. So wie wir im täglichen Leben eine Distanz messen, in dem wir die Meter zählen, die wir zurück legen müssen, um von einem Ort zum anderen zu gelangen, so misst man die Anzahl der Bits, die man ändern muss, um von einer Bitfolge zur nächsten zu gelangen in der Hamming-Distanz.

Aber bei allem Verständnis für den guten alten Hamming und seine Distanzen, der aufmerksame Leser wird sich inzwischen natürlich eines ganz besorgt fragen: Was hat das eigentlich alles mit unserem Hypercube zu tun? Nun ja, sagen wir mal so, man bedient sich der Hamming-Distanz als Hilfsmittel für seine Darstellung. Und zwar mit Hilfe der Nummerierungen der Ecken und ihrer Auswertung in Diagrammen. Letztendlich ist das Darstellen höherdimensionaler Körper nur ein Zählspiel, passt auf! 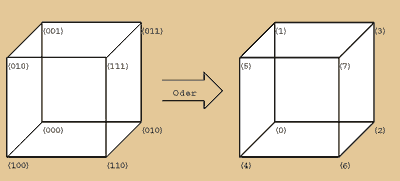Wir üben das lieber noch einmal bei der uns durchaus vertrauten dritten Dimension und seinem dazugehörigen Würfel. Zuerst nummerieren wir die Ecken unseres Würfels mit Hilfe so genannter Koordinatentrippel. Wir können diese Nummerierung natürlich auch im Dezimalsystem vornehmen, das ist vollkommen egal.

(0,0,0) im linken Beispiel oder (0) im rechten bilden dabei unseren Würfel- und Koordinatenursprung. Diese definierten Eckpunkte unseres Würfels, egal, wie wir sie benannt haben, tragen wir senkrecht in unserem Koordinatensystem ab. Wir erinnern uns: Ecken, die vom Ursprung gesehen nur eine Strecke entfernt liegen haben die Hamming-Distanz eins. Ecken mit einem Abstand von zwei Strecken haben die Hamming-Distanz zwei. Und genau diese Werte bilden die Waagrechte in unserem Koordinatensystem. 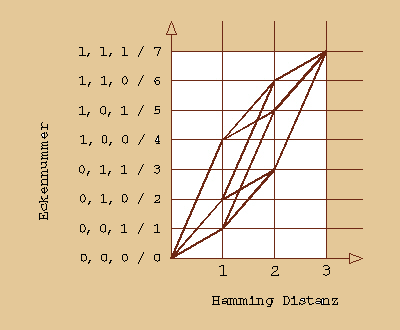Wir tragen nun die Eckpunkte unseres Körpers ein und verbinden vom Ursprung angefangen immer die Punkte miteinander, die die Hamming-Distanz eins haben. Und siehe da, wir erhalten ein einwandfreies Würfelbild!

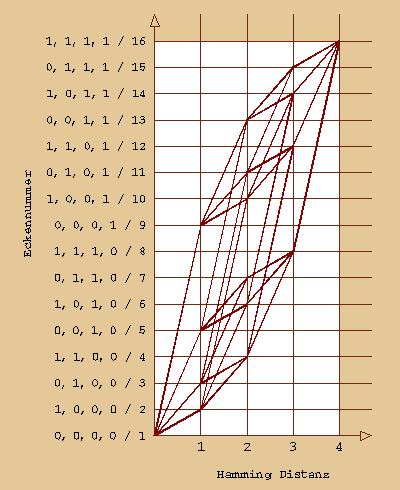
Und hier kommt uns wieder einmal mehr zu Gute, dass man alles, was sich in höheren Dimensionen abspielt und sich in unseren Köpfen einfach nicht vorstellen lassen will, auf einem Blatt Papier analysieren und ausrechnen lässt. Wir können dieses Prinzip nämlich auf den vierdimensionalen Raum übertragen, indem wir einfach die Eckpunkte unseres Hyperwürfels (die diesmal natürlich aus einer Viererkombination bestehen) in das Koordinatensystem zu übertragen und wieder die Einser-Hamming-Distanzen miteinander zu verbinden und schon haben wir ihn vor unserem dreidimensionalen Auge: den HYPERCUBE!

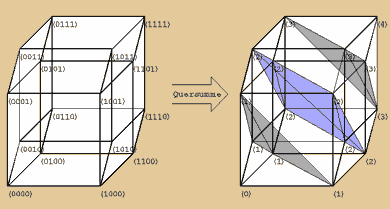
Aber Gott sei Dank können wir mit den Eckkoordinaten auch noch ein bisschen weiter spielen. Was ich z.B. immer sehr gern mache, ist erst mal eine Quersumme bilden. In diesem Fall erhalten wir für jede Koordinate eine Zahl von null bis vier. Die Null und die Vier stehen jeweils alleine an den sich gegenüber liegenden äußeren Eckpunkten. Wenn wir nun alle gleichen Zahlen miteinander verbinden, sehen wir erstaunliches. Die Einsen und Dreien ergeben jeweils ein Tetraeder, wenn man sie verbindet und die Zweien bilden in der Mitte des Hypercubes ein Oktaeder.