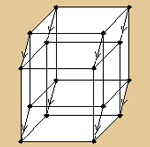
Wenden wir uns jedoch jetzt dem Hypercube selbst zu. Wie können wir ihn nun darstellen? Wir waren beim Würfel stehen geblieben. Wir schummeln einfach noch ein bisschen weiter und verschieben auch ihn parallel im Raum und verbinden alle seine Ecken. Und jetzt haben wir die Parallelprojektion des Hypercubes!

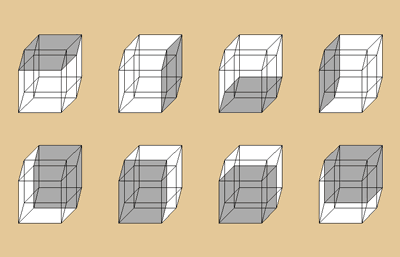
In einem vierdimensionalen Hyperwürfel wohnen acht dreidimensionale Würfel. Dem geschulten Auge mögen sie sich beim Betrachten recht schnell zeigen. Dem Sehorgan der weniger geschulten Sorte, kann dies mit etwas Geduld und unter Verlust von einiger Tränenflüssigkeit auch gelingen. Doch wir können es uns natürlich auch etwas leichter machen, indem wir die einzelnen Würfel einfach farbig markieren. So kann man sich dann in etwa eine Vorstellung darüber machen, was in einem solchen Gebilde so abgeht.

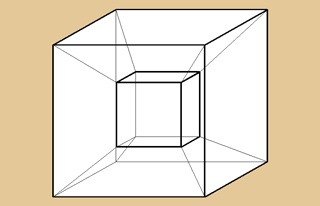
In der Zentralprojektion erscheinen sechs der acht Würfel des Hypercubes verzerrt und sehen deshalb aus wie Trapeze oder Pyramidenstümpfe. Im gesamten Internet wird erzählt, dass diese Darstellung des Hypercubes, die wir auch auf der Indexseite finden, auf Viktor Schlegel zurückgeht. Ich weiß nicht, wer Viktor Schlegel ist, ich hab’s bisher auch nicht rausbekommen. Ich versuche es natürlich weiterhin... Wenn Ihr es wisst, könnt Ihr mir gern schreiben. Ich freue mich! Also, wer nun auch immer Viktor Schlegel gewesen sein mag, seine Zentralprojektion sehen wir noch mal hier:

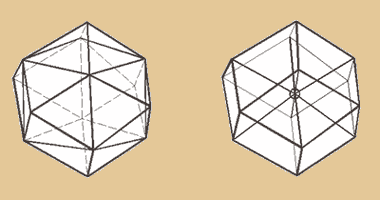
Für alle, die sich vielleicht auch schon für die archimedischen und catalanischen Körper erwärmen konnten und die noch ein bisschen staunen wollen: Wenn wir uns die Perspektive eines Rhombendodekaeders schnappen und die Ecken, des ehemaligen Würfels alle mit dem Mittelpunkt verbinden, dann haben wir die Isometrische Darstellung des vierdimensionalen Hyperwürfels vor uns. Klingt verrückt, ist aber so... ;-)