| |
 |
|
|
Die Natur zeigt uns nur
den Schwanz des Löwen. (oder des Geparden?)
Aber ich zweifle nicht daran, dass dazu ein Löwe
gehört, obwohl er sich uns wegen seiner enormen
Größe nicht gänzlich enthüllen
kann.
Albert Einstein
|
Um der Vereinigung der Grundkräfte
im Hyperraum näher zu kommen, benötigen
wir dazu das mathematische Prinzip der Feldtheorie.
Denn sie ist die universelle mathematische Sprache
der Physik. Eingeführt hat die Felder Michael
Faraday im 19. Jhd. Er stellte sich Kraftlinien
vor, die in alle Richtungen, ähnlich wie
die Ranken einer Pflanze, aus Magneten und elektrischen
Ladungen in den Raum hinein wachsen und ihn ausfüllen.
So vermochte er zum Beispiel jedem beliebigen
Punkt im Raum mit nur drei Zahlen die Richtung
und die Stärke der Kraft zuzuweisen. Die
Gesamtheit dieser Zahlen an jedem Punkt im Raum
als eine Einheit betrachtet bezeichnete er als
Feld. Dieses Feldkonzept ist deshalb so leistungsfähig,
weil sich alle Naturkräfte in diesen Feldern
ausdrücken lassen. Nur eines fehlte noch:
Die Gleichungen, denen diese Felder gehorchen!
Die Fortschritte der letzten hundert Jahre in
der theoretischen Physik lassen sich eigentlich
kurz und bündig mit der Suche nach den Feldgleichungen
beschreiben. James Clerk Maxwell entwickelte um
das Jahr 1860 herum die Feldgleichung für
Elektrizität und Magnetismus. 1915 entdeckte
Albert der Einstein die Feldgleichung für
die Gravitation. Und in den 1970er Jahren gelangte
man endlich zu den Feldgleichungen der subatomaren
Kräfte, die C.N. Yang und sein Student R.L.
Mills bereits 1954 entdeckt hatten. Es ist dies
die Verallgemeinerung des Maxwellschen Feldes,
welches das Licht beschreibt. Allerdings hat das
Yang-Mills-Feld sehr viel mehr Bestandteile und
kann eine elektrische Ladung besitzen, während
das Photon keine solche Ladung trägt. Die
klügsten Köpfe der Physik haben versucht
all diese Feldgleichungen zu vereinen und sind
gescheitert. Die Einsteinsche Gravitationsfeldgleichung
scheint so viel anders zu sein als die subatomare.
Wir stehen also wieder vor dem Gepardenkäfig.
Unsere drei Dimensionen reichen nun einmal nicht
aus, um alle Gleichungen in ihnen zu vereinigen.
Mit der Hyperraumtheorie lassen sich das Yang-Mills-Feld,
das Maxwellsche und das Einsteinsche Feld bequem
im Hyperraum unterbringen. Dort fügen sie
sich wie die Teile eines Puzzles ineinander.
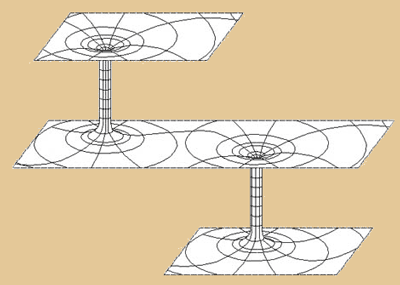
Doch für noch etwas anderes, verblüffendes
ist die Feldtheorie nützlich. Mit ihrer Hilfe
können wir exakt berechnen, wieviel Energie
nötig ist, um in Raum und Zeit Wurmlöcher
zu bilden, um die Raum-Zeit zu tunneln und damit
Reisen durch dieselbe möglich zu machen.
|
 |
|
Wir besitzen also die mathematischen Vorraussetzungen,
um Maschinen zu bauen, die Raum und Zeit nach
Belieben krümmen können, aber beileibe
nicht die Energie dazu, dies auch wirklich zu
tun. Wann dies soweit sein wird, dazu kommen wir
später. Zunächst wollen wir sehen, wie
die Mathematik in ihren zweitausend Jahre alten
Schuhen dahin kam, auf dem Parkett der höheren
Dimensionen zu tanzen.
Dies verdanken wir Bernhard Riemann, der in seiner
berühmten Lesung an der Universität
Göttingen am 10. Juni 1854 eine neue Geometrie
geboren hat. Mit einem Geniestreich machte er
die Welt mit den fantastischen Eigenschaften des
Hyperraums vertraut. Und es war, als lasse er
helles Sonnenlicht in ein dunkles, muffiges Zimmer.
Er brachte die Stützpfeiler der griechischen
Geometrie zum Einsturz, die solange den Angriffen
aller Skeptiker standgehalten hatte. Die alte
Geometrie des Euklid, in der alle geometrischen
Figuren zwei- oder dreidimensional sind, brach
zusammen und aus ihren Ruinen entstand die neue
Riemannsche Geometrie. Das klingt alles sehr einfach,
aber in anbetracht dessen, dass Euklids „Elemente“
nach der Bibel wohl das einflussreichste Buch
aller Zeiten gewesen sein dürfte, war es
das doch sicher nicht. Es sei ja wohl offenkundig,
sagte Euklid selbst, dass ein Punkt keinerlei
Dimension habe. Eine Linie hat eine Dimension
– die Länge. Eine Ebene besitzt zwei
– Länge und Breite. Ein fester Körper
hat drei – Länge, Breite und Höhe.
Und damit Schluss. Der Astronom Ptolemäus
von Alexandrien setzte 150 n. Chr. Noch einen
drauf. In seinem Buch „Über Entfernung“
erklärte er höchst einfallsreich, warum
die vierte räumliche Dimension nicht möglich
sei. Man solle drei Linien zeichnen, die alle
senkrecht zueinander stehen, so wie die Ecke eines
Würfels gebildet wird. Und dann solle man
versuchen, eine vierte Linie, die ebenfalls senkrecht
zu allen anderen steht, zu zeichnen, um festzustellen,
dass dies beim besten Willen nicht möglich
sei. Damit war für ihn die Sache klar. Doch
bewiesen hat Ptolemäus damit eigentlich etwas
anderes. Dass wir uns nämlich mit unserem
dreidimensionalen Hirn nur einfach keine Vorstellung
von der vierten Dimension machen können.
Denn schließlich wissen wir heute, dass
sich sehr viele Objekte in der Mathematik zwar
nicht sichtbar machen, wohl aber beweisen lassen.
|
| |
Riemann erschien Euklids Geometrie zu einfach
und steril gegenüber der ganzen Vielfalt
der Welt. Gebirgsketten, Meereswellen, Wolken
und Strudel sind nun mal keine vollkommene Kreise,
Dreiecke oder Quadrate, sondern gekrümmte
Objekte, die sich in unendlicher Vielfältigkeit
biegen und verdrehen. Er begann in der zweiten
Dimension. Er stellte sich ein flaches Blatt Papier
vor, auf dem Bücherwürmer flach vor
sich hin lebten. Nun ging er einen Schritt weiter.
Er setzte die Würmer auf ein zerknittertes
Blatt Papier. Was dächten die Würmer
über ihre Welt? Natürlich wären
auch sie der Meinung ihre Welt sei vollkommen
flach. Doch beim Kriechen über die verknitterte
Oberfläche würden sie eine geheimnisvolle,
unsichtbare Kraft spüren, die sie daran hinderte
sich in gerader Linie fort zu bewegen, da ihr
Körper stets nach links oder rechts gedrückt
würde.
Nach zweihundert Jahren war Riemann
der erste Wissenschaftler, der sich über
Newtons Fernwirkungsprinzip hinwegsetzte. Für
ihn wirkte die Kraft nicht unerklärlicherweise
von irgendwoher, sondern war einfach eine Konsequenz
der Geometrie. Nun ersetzte er das Blatt Papier
durch unsere dreidimensionale Welt, die in der
vierten räumlichen Dimension zerknittert
ist. Auch wir merken nicht, dass unsere Welt gekrümmt
ist. Auch bei uns stimmt etwas nicht, da wir uns
mit den geheimnisvollen, unsichtbaren Kräften,
wie Magnetismus und Gravitation auseinander setzen
müssen. Riemann gelangte also zu dem Schluss,
dass diese Kräfte kein unabhängiges
Eigenleben besitzen, sondern durch Verwerfung
(Knittern) unseres Universums in der vierten räumlichen
Dimension hervorgerufen werden.
Wie wir inzwischen wissen, gehört
zu jeder wissenschaftlichen Entdeckung auch eine
Gleichung, durch die diese sich beschreiben lassen
muss, sonst hat die beste Entdeckung keinen Wert.
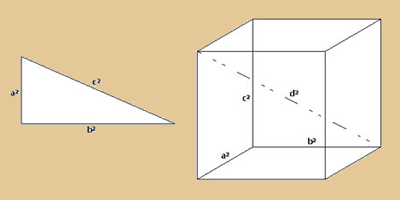
Hier setzte Riemann beim Satz des Pythagoras an.
Jedes Bauwerk unseres Planeten folgt diesen Gesetzen.
Ohne Schwierigkeiten lässt sich dieser Lehrsatz
in den dreidimensionalen Raum übertragen:
|
|
| |
|
Die Summe der Quadrate von drei anliegenden Kanten
eines Würfels sind gleich dem Quadrat der
Diagonale durch den Würfel, also a²
+ b² + c² = d². Dieses Spiel lässt
sich nun beliebig fortführen. Wenn a, b,
c, d, e.... die Kanten des Hyperwürfels sind
(mal davon abgesehen, dass wir ihn uns nicht vorstellen
können) und z die Länge seiner Diagonalen,
so ist a² + b² + c²+ d² +e²...
= z².
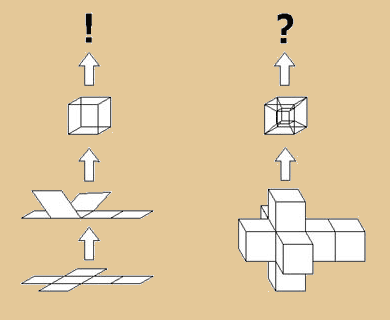
Hier muss ich kurz etwas einschieben, was Euch
vielleicht hilft, Euch die Unvorstellbarkeit besser
vorzustellen. Oder auch nicht. ? Also, „Flachländer“
z.B. können sich ja auch keine Vorstellung
von einem dreidimensionalen Würfel machen,
wohl aber eine begriffliche, nämlich indem
sie ihn auffalten. Dann sieht der Würfel
für einen Flachländer aus wie ein Kreuz,
das aus sechs Quadraten besteht. Entsprechend
können wir uns ja nun bedauerlicherweise
keine Vorstellung vom besagten vierdimensionalen
Hyperwürfeln machen. Doch wenn wir ihn auffalten,
dann erhalten wir das dreidimensionale Pendant
zum Kreuz, den so genannten Tesseract. LINK HYPERCUBE
|
|
|
Das ist das Verrückte am Hyperraum. Auf einem
zweidimensionalen Blatt Papier können wir
ohne Probleme die Eigenschaften höherdimensionaler
Objekte beschreiben und anwenden, von denen sich
unser dreidimensionales Gehirn keine Vorstellung
machen kann.
Da Riemann ein neues Objekt in die Mathematik
einführen wollte, mit dessen Hilfe sich alle
Flächen, ganz gleich wie kompliziert oder
gekrümmt sie waren, beschreiben lassen, musste
er geradezu zwangsläufig auf Faradays Feldkonzept
zurückgreifen. Wir erinnern uns: Faraday
wies jedem Punkt im Raum drei Zahlen zu, um die
magnetische und elektrische Kraft an diesem Punkt
zu beschreiben. Riemann ordnete nun jedem Punkt
im Raum eine Reihe von Zahlen zu, die angeben,
wie er verworfen oder gekrümmt ist. Dies
ist heute der berühmte Riemannsche Maßtensor.
Grundsätzlich ist die Verformung umso größer,
je höher der Wert des Tensors. Das „Blatt“
kann noch so zerknittert sein - mit dem Maßtensor
steht uns ein einfaches Mittel zur Verfügung,
seine Krümmung an jedem Punkt im Raum zu
messen. Würden wir das Blatt wieder vollständig
glätten, kämen wir auf den Satz des
Pythagoras zurück. Doch obwohl er uns mit
seinem Maßtensor ein leistungsfähiges
Mittel für die Beschreibung des gekrümmten
Raumes in die Hand gab, wusste er nicht genau,
welchen Gleichungen nun der Maßtensor selbst
gehorchte. Das heißt auf gut Deutsch: Ihm
war nicht klar, was das Blatt zerknitterte.
Aus gutem Grund werde ich nun auf einen Streifzug
durch die Jahrzehnte der Physik, welcher den unendlich
langen Mittelteil des Buches bildet, verzichten.
In diesem Teil suchten unermüdliche Forscher
nach einer Theorie, mit deren Hilfe sich die Kräfte
im Hyperraum vereinen ließen, und fanden
sie doch nicht. Ich muss gestehen, dass ich es
sehr schwer hatte, mich durch den Dschungel der
erfolglosen Hypothesen zu kämpfen. Detaillierte
Ausführungen über das Standardmodell,
GUT´s, Supergravitation und Störungsrechnungen
begleiteten mich mehrere Wochen jeden Abend, ohne
dass ich behaupten kann, sie alle wirklich verstanden
zu haben. Der Autor selbst erwähnte hierzu,
natürlich könne man erkennen, dass sich
aus der Superstringtheorie (was zur Zeit die Créme
der Hochenergiephysik ist) die Supergravitation,
die Kaluza-Klein-Theorie usw. ableiten lasse,
und sogar das baden gegangene Standardmodell finde
sich in ihr wieder, doch man wisse nicht wie es
dazu kommt. Dazu sei momentan noch niemand intelligent
genug. Ich weiß nicht wie es Euch geht,
aber mich tröstet das. Obwohl es absolut
nicht uninteressant war, dank der anschaulichen
Erzählweise von Herrn Kaku, beim Bau von
superempfindlichen Detektoren, die den totalen
Zerfall von Protonen aufzeichnen sollten und Atomzertrümmerer
praktisch selbst anwesend zu sein, verzichte ich
hier auf eine Wiedergabe all dessen. Wer also
auf ausführlichste Erklärungen nicht
verzichten kann, was die Quarks nun wirklich mit
den Leptonen machen, und warum die Neutrinos doch
nicht die kleinsten Teilchen im Universum sind,
der wird nicht umhin kommen, dies wunderbare Buch
selbst zu lesen.
Ich möchte lieber an der Stelle weitermachen,
an der endlich die Themen zur Sprache kommen,
die uns alle interessieren: Krümmung der
Raum-Zeit und damit Reisen durch den Hyperraum,
was nichts anderes heißt als Reisen durch
Raum und Zeit. Bei diesem Stichwort fällt
mir ein guter, alter Bekannter aus dem Buch ein:
der Plattwurm Kolumbus. Herr Kaku hat ihn wohl
zum besseren Verständnis von Raum-Zeit-Reisen
erfunden, doch ich glaube es gibt ihn wirklich...
|
 |
|
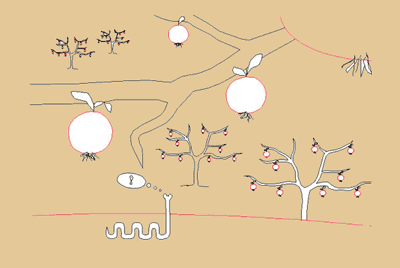
Auf der Oberseite eines Apfels lebt ein Volk von
winzig kleinen Plattwürmern. Natürlich
ist für diese Würmer ihre Welt, die
sie Apfelwelt nennen, vollkommen flach und zweidimensional
und so benehmen sie sich auch. Doch unter ihnen
lebt ein Revolutionär, der Wurm Kolumbus,
der besessen ist von der Vorstellung, die Apfelwelt
sei endlich und in etwas gekrümmt, was er
dritte Dimension nennt. Dafür erfindet er
sogar zwei neue Worte, die er „oben“
und „unten“ nennt, um die Bewegungen
in dieser dritten Dimension zu beschreiben. Seine
Freunde indes halten ihn für einen Narren.
„Kolumbus, Du spinnst.“ sagen sie.
Eines Tages aber macht sich Kolumbus auf eine
lange mühsame Reise, auf der er immer nur
geradeaus kriecht. Er kriecht und kriecht, verschwindet
hinter dem Horizont und gelangt schließlich
zu seinem Ausgangspunkt zurück. Da er immer
nur geradeaus gekrochen war, beweist er damit,
dass die Apfelwelt tatsächlich in einer unsichtbaren
Dimension gekrümmt ist. Obwohl Kolumbus von
seinen Reisen sehr erschöpft ist, entdeckt
er, dass es noch weitere Möglichkeiten gibt,
auf dem Apfel zu reisen. Wenn er sich in den Apfel
gräbt, kann er einen Tunnel bohren und so
eine bequeme Abkürzung zwischen zwei weit
entfernten Punkten herstellen. Diese Tunnel nennt
er Wurmlöcher. „g“ Seine bedeutendste
Entdeckung jedoch, haut Kolumbus fast selbst vom
Hocker: Seine Apfelwelt ist nicht die einzige
im Universum, sondern nur ein Apfel in einem riesigen
Apfelgarten. Es gibt noch hunderte, vielleicht
tausende weitere Äpfel, manche mit Würmern,
wie ihm selbst, manche ohne. Unter bestimmten
Umständen, so mutmaßt er, müsste
sogar eine Reise zwischen den verschiedenen Äpfeln
des Obstgartens möglich sein...
|
->
Einstein's Geist
|
|
|
|
|
 |
| |
|
|
 |
Im
Feld der Theorien |
|
|
|
|
| |
| |
|