Symmetrie
Jeder Platonische Körper besitzt verschieden
viele Symmetrie- oder auch Drehachsen. Und die
jeweilige Lage der Achse bestimmt, wie viele Drehungen
notwendig sind, um den Körper wieder in seine
Ausgangsposition zu bewegen. Bei einer dreizähligen
Drehachse muss der Körper zwei Drehungen
vollführen, bei einer vierzähligen Drehachse
drei Drehungen. Nach dem Zusammenzählen aller
möglichen Drehungen addieren wir noch eine
Drehung, die ihn in seine Ausgangsposition zurückführt.
|
Tetraeder
|
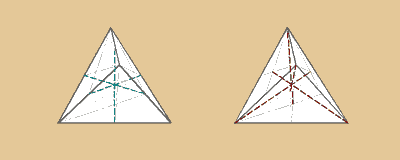
Jede der 4 Seitenflächen kann auf die Grundfläche
gesetzt werden und dies in 3 Positionen - also
gibt es 4 • 3 = 12 Positionierungen auf
der Grundfläche.
Tetraeder Drehachsen:
3 zweizählige (durch die Mittelpunkte je
2 gegenüberliegender Kanten)
4 dreizählige (durch die Ecken und Mittelpunkte
der jeweils gegenüberliegenden Seitenflächen)
4 • 2 + 3 • 1 + 1 = 12 Drehungen
|
Hexaeder |

|
6 • 4 = 24 Positionierungen auf der Grundfläche
Hexaeder Drehachsen:
6 zweizählige (durch Mittelpunkte je 2 gegenüberliegender
Kanten)
4 dreizählige (durch je 2 gegenüberliegende
Ecken)
3 vierzählige (durch Mittelpunkte je 2 gegenüberliegender
Seitenflächen)
4 • 2 + 6 • 1 + 3 • 3 + 1 = 24
Drehungen
|
|
Okteder |
|
8 • 3 = 24 Positionierungen auf der Grundfläche
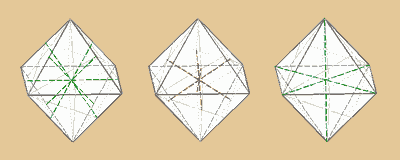
Oktaeder Drehachsen:
6 zweizählige (durch Mittelpunkte je 2 gegenüberliegender
Kanten)
4 dreizählige (durch Mittelpunkte je 2 gegenüberliegender
Seitenflächen)
3 vierzählige (durch je 2 gegenüberliegende
Ecken)
3 • 3 + 6 • 1 + 4 • 2 + 1 = 24
Drehungen
|
|
Dodekaeder
|
|
12 • 5 = 60 Positionierungen auf der Grundfläche
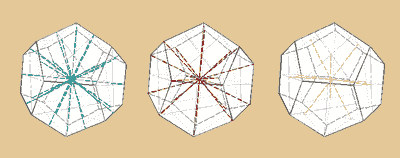
Dodekaeder Drehachsen:
15 zweizählige (durch Mittelpunkte je 2 gegenüberliegender
Kanten)
10 dreizählige (durch je 2 gegenüberliegende
Ecken)
6 fünfzählige (durch Mittelpunkte je 2
gegenüberliegender Seitenflächen)
10 • 2 + 15 • 1 + 6 • 4 + 1 = 60
Drehungen
|
|
Ikosaeder
|
|
20 • 3 = 60 Positionierungen auf der Grundfläche
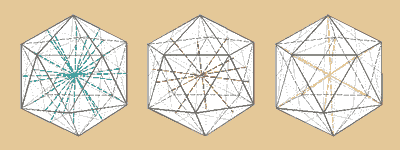
Ikosaeder Drehachsen:
15 zweizählige (durch Mittelpunkte je 2 gegenüberliegender
Kanten)
10 dreizählige (durch Mittelpunkte je 2 gegenüberliegender
Seitenflächen)
5 fünfzählige (durch je 2 gegenüberliegende
Ecken)
6 • 4 + 15 • 1 + 10 • 2 + 1 = 60
Drehungen
|
|