Die
Archimedischen Körper
Archimedische Körper sind so genannte halbreguläre
Körper. Auch sie haben regelmäßige
Polygone als Begrenzungsflächen, lassen aber
Flächen mit unterschiedlicher Eckenanzahl
zu. Das allein macht aber noch keinen Archimedischen
Körper, denn von dieser Art gibt es unendlich
viele und dementsprechend wäre das ja auch
nichts besonders. Nein, die Kantenlängen
müssen auch noch alle gleich lang sein. Und
außerdem muss jede Ecke des Polyeders durch
eine seiner Symmetrieoperationen auf jede andere
Ecke abgebildet werden können. Das klingt
ganz schön kompliziert, heißt aber
nichts anderes, als dass ich einen Archimedischen
Körper von einer Ecke auf eine andere drehen
kann und er hinterher genau so aussieht wie vorher.
Das nennt man die Uniformität der Ecken.
Faszinierend! Und wenn man all diese Bedingungen
gemeinsam anwendet, bleiben von einem ganzen Haufen
Prismen und Antiprismen nur die 13 Archimedischen
Körper übrig. Zu allem Überfluss
können diese nun auch noch auf recht unterschiedliche
Weise entstehen. Die meisten haben allerdings
irgendwas mit wegschneiden und abschnippeln oder
fachmännisch: abstumpfen, zu tun.
Unsere erste Gruppe z.B. Man erkennt sie natürlich
sofort, das sind quasi die ehemaligen Platonischen
Körper. Wenn wir von denen nämlich
die Ecken wegschneiden, dann haben wir schon
fünf von dreizehn Körpern im Sack.
|
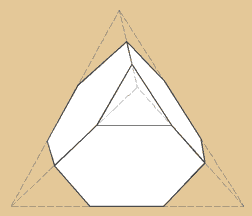
Abgestumpftes Tetraeder
Das abgestumpfte Tetraeder hat insgesamt nur 8
Grundflächen und ist damit der Archimedische
Körper mit den wenigsten Grundflächen.
Die 8 Flächen teilen sich in jeweils 4 Dreiecke
und 4 Sechsecke auf. Das abgestumpfte Tetraeder
hat 12 Ecken und 18 Kanten. |
|
|
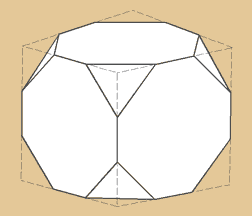
Abgestumpftes Hexaeder
Ein abgestumpftes Hexaeder besitzt insgesamt 14
Grundflächen. Sie bestehen aus 8 Dreiecken
und 6 Achtecken. Und dann sind da noch die 24
Ecken und 36 Kanten.
|
 |
|
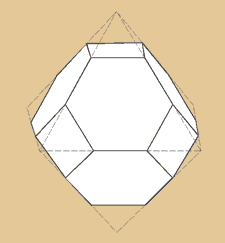
Abgestumpftes Oktaeder
Die ebenfalls 14 Flächen des abgestumpften
Oktaeders sind 8 Sechsecke und 6 Quadrate. Ebenso
wie der Hexaederstumpf hat es 24 Ecken und 36
Kanten.
|
|
|
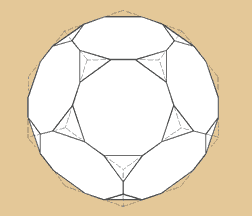
Abgestumpftes Dodekaeder
Das abgestumpfte Dodekaeder besteht aus 32 Grundflächen,
nämlich aus 20 Dreiecken und 12 Zehnecken.
Es hat 60 Ecken und 90 Kanten.
|
|
|
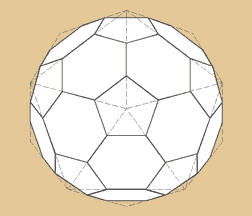
Abgestumpftes Ikosaeder
Die Gesamtgrundflächenanzahl bei diesem Archimedischen
Körper beträgt 32, bestehend aus 12 Fünfecken
und 20 Sechsecken. Das Abgestumpfte Ikosaeder hat
auch 60 Ecken und 90 kanten. Wir kennen ihn als
Fußball.
|
|
|
Die zweite Gruppe, wie ich sie mal hier
nenne, ist in ihrer Entstehung auch noch leicht
vorstellbar. Wir nehmen die jeweils dualen platonischen
Körper (also Würfel und Oktaeder, sowie
Dodekaeder und Ikosaeder), stecken sie ineinander
und schneiden alles ab, was übersteht. Diese
Verschmelzungen nennen sich bezeichnender Weise
Kuboktaeder und Ikosidodekaeder. Auch da kommt
man noch ganz gut mit…
|
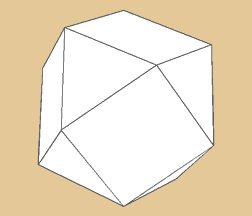
Kuboktaeder
Aus Verschmelzung von Würfel und Oktaeder
erhalten wir den Kuboktaeder (auch Vektorequilibrium
genannt). Es besteht aus 6 Quadraten und 8 Dreiecken,
also insgesamt 14 Grundflächen. Er hat 12
Ecken und 24 Kanten.
|
|
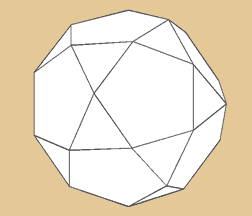
Ikosidodekaeder
Aus der Verschmelzung von Ikosaeder und Dodekaeder
erhalten wir das Ikosidodekaeder. Es hat 32 Flächen,
nämlich 20 Dreiecke und 12 Fünfecke. Dazu
gibts in diesem Beispiel 30 Ecken und 60 Kanten.
|
|
Die nächste Gruppe wird aus den Abstumpfungen
der vorherigen beiden Körper gebildet. Wir
sehen also, Ecken abschneiden ist bei der Entstehung
der Archimedischen Körper ganz schön angesagt.
|
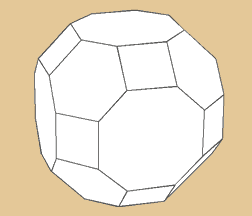
Abgest.Kuboktaeder oder Großes Rhombenkuboktaeder
Dieser Archimedische Körper setzt sich als
erster aus drei verschiedenen Grundflächen
- insgesamt 26 - zusammen. Als da wären 12
Quadrate, acht Sechsecke und sechs Achtecke. Hier
gibt es 48 Ecken und 72 Kanten.
|
|
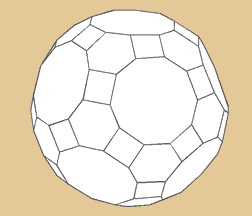
Abges. Ikosidodekaeder
oder gr. Rhombenikosidodekaeder
Das Große Rhombenikosidodekaeder besitzt
62 Flächen, die sich aus verschiedenen zusammen
setzen, nämlich 30 Quadrate, 20 Sechsecke
und 12 Zehnecke. Außerdem hat es 120 Ecken
und 180 Kanten. Ganz schön viele...
|
|
Die nächsten beiden sind schon ein bisschen
schwieriger zu erklären.
|
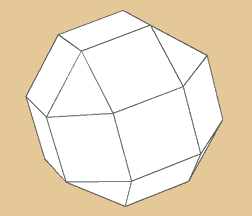
Kleines Rhombenkuboktaeder
Das kleine Rhombenkuboktaeder besteht wieder nur
aus zwei verschiedenen und insgesamt 26 Grundformen
und setzt sich aus 8 gleichseitigen Dreiecken
und 18 Quadraten zusammen. Es hat 24 Ecken und
48 Kanten.
|
|
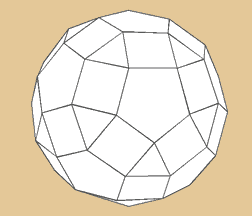
Kleines Rhombenikosidodekaeder
Seine Oberfläche setzt sich aus drei verschiedenen
regelmäßigen Vielecken zusammen. Seine
insgesamt 62 Grundflächen bestehen aus 20
Dreiecken, 30 Quadraten und 12 Fünfecken.
Begrenzt wird das ganze von 60 Ecken und 120 Kanten.
|
|
Bei unseren letzten beiden Experten spielt das
Abschneiden endlich mal keine Rolle. Hier wird
mal nichts weggenommen, sondern einfach was dazu
getan. Dreiecke nämlich. Wie ein Cubus Simus
entsteht, stellt man sich am besten so vor: Wir
“sprengen“ einen Würfel so, dass
alle Quadratecken von einander getrennt sind.
Die Flächen werden nun mittels Dreiecken
miteinander verbunden, dass sich an jeder Ecke
vier Dreiecke und ein Quadrat treffen (3334).
Es sind also 32 Dreiecke und sechs Quadrate. Bei
60 Kanten und 24 Ecken bedeutet das, dass die
Eulersche Charakteristik (24+38-60=2) erfüllt
ist.
|
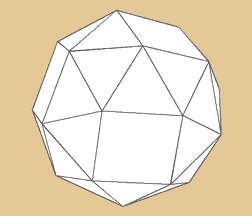
Abgeschrägtes Hexaeder
oder Cubus simus
Ein abgeschrägtes Hexaeder besteht aus zwei
verschiedenen Arten und insgesamt 38 Grundflächen.
Als da wären 32 Dreiecke und 6 Quadrate.
An einer Ecke treffen sich immer vier Dreiecke
und ein Quadrat. Mit 24 Ecken und 60 Kanten ist
er anzahlmäßig hier eher gutes Mittelmaß.
|
|
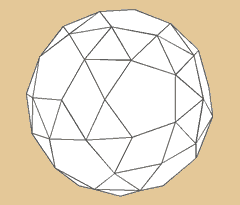
Abgeschrägtes Dodekaeder
oder Dodekaedron simum
Das abgeschrägte Dodekaeder wiederrum setzt
seine 92 Grundflächen, aus 80 Dreiecken und
12 Fünfecken zusammen. Und natürlich
auch aus 60 Ecken und 150 Kanten.
|
|
Beim abgeschrägten Hexaeder
und beim abgeschrägten Dodekaeder
handelt es sich um sodenannte chirale Körper.
Das heißt sie kommen in zwei spiegelbildlichen
Varianten vor, die sich nicht durch Drehungen
zur Deckung bringen lassen. Johannes Kepler hat
sie in seinem Buch "Harmonice Mundi“,
das 1619 in Linz erschienen ist, genauer untersucht
und insbesondere die Vollständigkeit der
obigen Aufzählung bewiesen. Er nannte sie
"Cubus simus" bzw.
"Dodecahedron simum".
Simus heißt hier wörtlich: plattnasig.
Weil manche auch die beiden Spiegelbilder aus
der abgeschrägten Fraktion als eigenständigen
Körper sehen, hört/liest man manchmal
auch von 15 archimedischen Körpern. Also,
nicht durcheinander bringen lassen... ;-)
|