Die
Catalanischen Körper
Catalanische Körper verhalten sich polar
oder dual zu den Archimedischen Körpern.
Ihren Namen haben sie von dem belgischen Mathematiker
Eugène Charles Catalan, sie werden aber
auch oft Dual-Archimedische Körper genannt.
Im Unterschied zu den “richtigen“
Archimedischen Körpern bestehen die Catalanischen
nur aus einer Flächenart, nämlich identischen
Rauten bzw. Rhomben. Dafür lassen sie aber
(wiederum ein Unterschied zu den Archimedischen)
pro Ecke eine verschiedene Anzahl von Kanten zu.
Das Rhombendodekaeder hat z.B. Ecken an denen
drei Rhomben (bzw. Kanten) und Ecken, an denen
vier Rhomben (bzw. Kanten) aufeinander treffen.
Damit ist es kein archimedischer Körper mehr.
Catalanische Körper entstehen (kompliziert
gesagt) durch die Umhüllung des Kerns eines
Archimedischen Körpers. Ich habe eine Weile
gebraucht, bis ich wusste, wie ich mir das vorstellen
muss. Ich bin anfangs sogar beim Selbstkonstruieren
durch Fehlinterpretationen von komplizierten Beschreibungen
in die Irre gelaufen. Deshalb will ich mal versuchen,
es an einem Beispiel so einfach wie nur möglich
zu erklären.
Wir rufen uns erst mal ins Gedächtnis, wie
das generell mit den Dualen Körpern war.
Zu jeder konstruierten Fläche gehört
also eine Ecke. Okay. Und dann erinnern wir uns
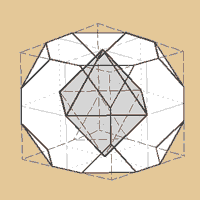
weiter, dass auf diese Weise im Innern eines Würfels
ein Oktaeder entstanden ist. Okay, wenn wir dieses
Spiel jetzt mit dem abgestumpften Hexaeder (also
quasi dem archimedischen Würfel) spielen,
sieht die Sache immer noch ganz ähnlich aus.
|
|
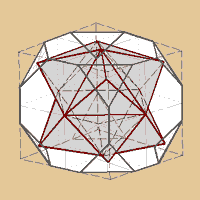
Allerdings
müssen wir jetzt noch bedenken, dass unser
Hexaederstumpf ja ein “paar Flächen
mehr“ hat, als sein Platonischer Bruder.
Also braucht sein Dualer Partner auch ein “paar
Ecken mehr“. Dazu stellen wir uns vor, wir
ziehen die Flächen des Oktaeders solange
von ihrem Mittelpunkt an nach außen, bis
dieser auf den Mittelpunkt der Dreiecksfläche
des Hexaederstumpfs trifft. |
 |
Und das war schon die ganze Kunst!
|
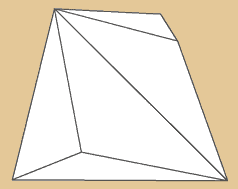
Triakis Tetrahedron
Das Triakis Tetraeder verhält sich dual zum
abgestumpften Tetraeder, hat insgesamt 12 Grundflächen
bestehend aus 4 x 3 Dreiecken, 8 Ecken und 18
Kanten.
|
|
|
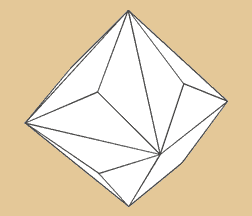
Triakis Oktahedron
Das Triakis Oktaeder verhält sich dual zum
abgestumpften Hexaeder. Es besitzt insgesamt 24
Grundflächen (8 x 3 Dreiecke), 14 Ecken und
36 Kanten.
|
|
|
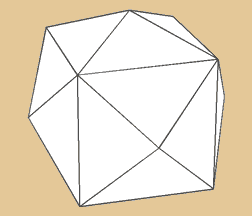
Tetrakis Hexahedron
Das Tetrakis Hexaeder verhält sich dual zum
abgestumpften Oktaeder. Es aus 24 Grundflächen,
14 Ecken und 36 Kanten. Die Grundflächen bilden
6 x 4 Dreiecke.
|
|
|
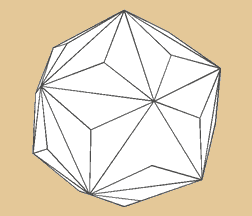
Triakis Ikosahedron
Das Triakis Icosaeder verhält sich dual zum
abgestumpften Dodekaeder. Seine 60 Grundflächen
teilen sich in 30 x 3 Dreiecke auf. Es besitzt
32 Ecken und 90 Kanten.
|
|
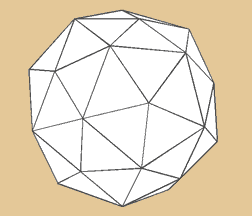
Pentakis Dodekahedron
Das Pentakis Dodecaeder verhält sich dual
zum Ikosaederstumpf. Es besitzt 60 Flächen
(bestehend aus 12 Fünfecken), 32Ecken und
90 Kanten. Der AIDS-Virus hat die Form eines Pentakis
Dodekaeders.
|
|
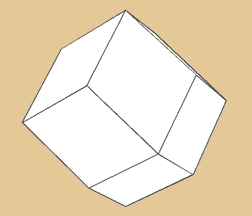
Rhombendodekahedron
Hier haben wir unseren ersten Catalanischen Körper,
der sich aus Rhomben zusammen setzt. Das Rhombendodekaeder
verhält sich dual zum Kuboktaeder. Es besteht
aus 12 Flächen, 14 Ecken und 24 Kanten. Er
ist der Hüllkörper der durch die Vereinigungsmenge
der Durchdringung eines Hexaeders (Kubus) und
Oktaeders beschrieben wird. An sechs der Ecken
grenzen vier Kanten und an die übrigen acht
Ecken grenzen drei Kanten.
|
|
Rhombentriakontahedron
Das Rhombentriacontaeder verhält sich dual
zum Ikosidodekaeder. Es besitzt 30 Flächen,
32 Ecken und 60 Kanten. Er ist der Hüllkörper
der durch die Vereinigungsmenge der Durchdringung
eines Dodekaeders und Ikosaeders beschrieben wird.
An 12 der Ecken grenzen 5 Kanten und an die übrigen
20 Ecken grenzen 3 Kanten an.
|
|
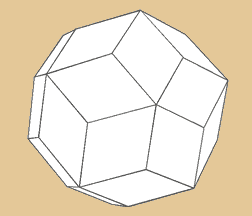
Disdyakis Dodekahedron,
Hexakis Oktahedron
Das Diydyakis Dodecaeder verhält sich dual
zum Abgestumpften Kuboktaeder. Es besitzt 48 Flächen,
26 Ecken und 72 Kanten. Seine Flächen bestehen
aus 8 x 6 Dreiecken.
|
|
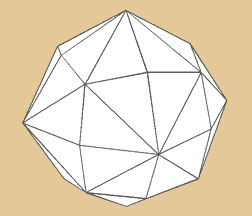
Disdyakis Triacontahedron,
Hexakis Ikosahedron
Das Disdyakis Triacontaeder verhält sich
dual zum abgestumpften Ikosaeder (Fußball).
Es besitzt insgesamt 120 Grundflächen, 62
Ecken und 180 Kanten. Er ist damit in unseren
Reihen der Körper mit den meisten Grundflächen,
die aus 12 x 10 Dreiecken bestehen.
|
|
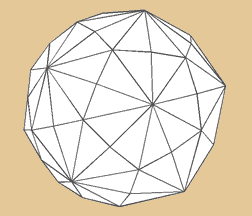
Trapezoid, Deltoid Ikositetrahedron
Das Deltoid-Icositetraeder verhält sich dual
zum Kleinen Rhombenkuboktaeder. Es besitzt 24
Flächen aus Rhomben, 26 Ecken und 48 Kanten.
|
|
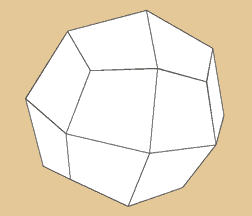
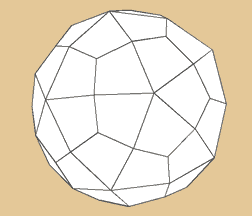
Trapezoid, Deltoid Hexacontahedron
Das Deltoid-Hexacontaeder verhält sich dual
zum Abgestumpften Ikosidodekaeder. Seine 60 Flächen
sind Rhomben. Dazu kommen 62 Ecken und 120 Kanten.
|
|
|
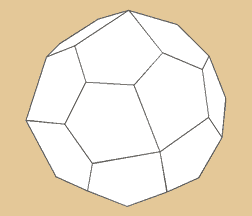
Pentagonal Ikositetraeder
Das Pentagonal-Icositetraeder verhält sich
dual zum Cubus Simus. Wie der Name schon verrät,
besteht er aus 24 Flächen. Und dann hat er
38 Ecken, woraus sich 60 Kanten ergeben. |
|
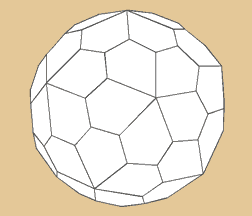
Pentagonal Hexacontaeder
Das Pentagonal-Hexacontaeder verhält sich
dual zum Dodekahedron Simum. Es besitzt 60 fünfeckige
Flächen, 92 Ecken und 150 Kanten.
|
|