Ich finde es höchst amüsant, dass der Goldene Schnitt bei unserem ersten Beispiel (es ist gleichzeitig unser umstrittenstes) gleich zweimal zuschlägt.
Beginnen wir mit der Lage der Pyramiden. In ihrem Buch “Das Geheimnis des Orion“ haben Robert Bauval und Adrian Gilbert sehr überzeugend dargelegt, dass die Pyramiden von Giseh den drei Gürtelsternen des Orion Al Nitak, Al Nilam und Mintaka entsprechen. Erweitert man den Untersuchungsradius rund um das Plateau, stellt man fest, dass sich auch andere Bauwerke und Tempelanlagen am Himmel über dem Nil wieder finden. Der Nil selbst begegnet uns am Himmel als Milchstraße. Das, was sich da vom Himmel spiegelt, nannten die Ägypter die unterirdische Duat. Die Duat war das dunkle Reich der Toten, dessen Herr Osiris war. Hier wurde die Wägung des Herzens vorgenommen, die jeder Verstorbene über sich ergehen lassen musste. Wenn er sie nicht bestand, durfte er seinen Weg nach Earu, dem lichten Endziel ihrer Reise nach dem Tod, nicht mehr fortsetzen, sondern musste hungernd und durstend in der Duat, deren Hieroglyphe übrigens ein fünfeckiger Stern ist, verbleiben.
Für die Ägypter war die Duat von unschätzbarer Wichtigkeit. Es verwundert deshalb nicht, dass wir die Himmelsduat in Stein gehauen auf der Erde wieder finden.
In der Abbildung können wir sehen, dass die drei Pyramiden außerdem noch auf einer Fibonacci-Spirale liegen. Sie zieht sich imaginär durch das Nildelta und beschreibt auf ihrem Weg noch weitere wichtige Bauwerke im Umland. Die Sphinx sitzt genau in der Mitte es Goldenen Kreuzes.

Wie stichhaltig dieses Beispiel ist, kann ich beim besten Willen nicht sagen. Für Richtigkeit kann ich keine Garantie übernehmen, aber immerhin die Erwähnung war es mir wert.
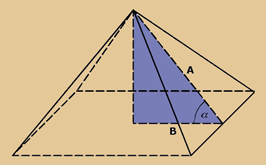
Die zweite Skizze soll zeigen, dass bei der großen Pyramide das Verhältnis der Schräge zur halben Breite 1.6185909090909090909090909090909 ergibt - das ist Phi in höchster Annäherung.

Wer sich mit der Konstruktion der Pyramiden und ihren mathematischen Zusammenhängen schon mal näher beschäftigt hat, wird jetzt vielleicht aufbegehren: “Moment mal, in den Bauten der Ägypter finden wir doch aber eine ganz andere Zahl, die zwar ganz ähnlich klingt, aber mit Phi im Grunde nichts zu tun hat!“ Mhhh… Vielleicht stimmt das ja nicht so ganz… Es gibt viele mathematische Spielereien, die hier darzulegen viel zu umfangreich wäre, die belegen, dass in den Konstruktionsmaßen der großen Pyramide ein Zusammenhang zwischen Phi und Pi besteht. Wer Lust drauf hat, sich diese Zusammenhänge näher zu betrachten, dem sei das Buch “Der Pyramidencode“ von Horst Bergmann und Frank Rothe empfohlen. Das ganze Buch ist sowieso eine phantastische Reise durch die Vergangenheit und allen Fans des Pyramidenbaus wärmstens empfohlen. Und im Anhang finden sich jede Menge ausführliche Beispielrechnungen. Unter anderem sehen wir, dass Phi2/5 = 0,523606797 ist, was eine ägyptische Königselle ist... Wer also nicht genug kriegen kann von mathematischen Zusammenhängen der antiken Art, der sollte sich dieses Buch ruhig geben, denn darauf jetzt genauer einzugehen, würde unseren Rahmen bei weitem sprengen.
Bei beiden gezeigten Beispielen (die Lage im Umland und das Verhältnis der Schräge der Pyramide zur halben Breite) ist nicht nachweisbar, ob die alten Ägypter tatsächlich Kenntnis vom Goldenen Schnitt hatten. Experten streiten sich darüber bis heute. Was dieses Thema angeht, sollte man vorsichtig sein. Natürlich ist es ratsam, immer kritisch zu bleiben und vor lauter Euphorie des Entdeckens nicht in alles, was einem begegnet den Goldenen Schnitt “hinein zu messen“. Andererseits haben wir bis heute nicht mal ansatzweise eine Vorstellung davon, was die Alten Kulturen vor über 4000 Jahren wirklich wussten. Was sie konnten, das sehen wir, aber wir sind nicht in der Lage, zu erklären, wie sie das geschafft haben. Zu meinen, die alten Ägypter konnten vom Goldenen Schnitt gar keine Ahnung gehabt haben, weil sie es nicht irgendwo für die Nachwelt hingekritzelt haben, erscheint mir ein wenig kurzsichtig. Und wo wir schon dabei sind.. Manchmal sieht man auch den Wald vor lauter Bäumen nicht.